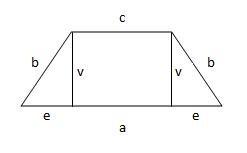
Isosceles trapezoid
Calculate the area of an isosceles trapezoid whose bases are at a ratio of 5:3. The arm is 6cm long and 4cm high.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Drainage channel
The drainage channel's cross-section is an isosceles trapezoid whose bases are 1.80 m and 0.90 m long, and the arm is 0.60 meters long. Calculate the channel's depth. - Perpendicular 32371
Calculate the area of a rectangular trapezoid whose perpendicular arm is 27 mm long and the bases are 33 mm and 19 mm long. - Isosceles trapezoid
Calculate the area of an isosceles trapezoid whose bases are in the ratio of 4:3; leg b = 13 cm and height = 12 cm. - Isosceles trapezoid
The bases of the isosceles trapezoid are in the ratio of 5:3. The arms have a length of 5 cm and height = 4.8 cm. Calculate the circumference and area of a trapezoid.
- Calculate 3161
In the isosceles trapezoid ABCD, the arm is 5.2 cm long, the middle bar is 7 cm long, and the height is 4.8 cm. Calculate the lengths of both bases. - Diagonal
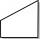The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm and CD = 4cm. Calculate the length of the AC diagonal. - Circumference 7823
The bases are 9 cm and 5 cm long in a rectangular trapezoid. The length of the shorter arm is 3 cm. Calculate its circumference and area.
