Trapezoid bases
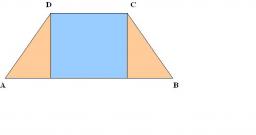
In the isosceles trapezoid ABCD, the arm is 5.2 cm long, the middle bar is 7 cm long, and the height is 4.8 cm. Calculate the lengths of both bases.
Final Answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
statisticsalgebraplanimetricsGrade of the word problem
Related math problems and questions:
- IS trapezoid
Isosceles trapezoid arm measured 80 cm. Height is 65 cm, and the middle segment is 71 cm. Find the length of its bases. - IS trapezoid
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Trapezoid side lengths
The circumference of the isosceles trapezoid is 34 cm. The difference in the length of the bases is 6 cm. The arm's length is one-third of the length of the longer base. Find the lengths of the trapezoidal sides. - Isosceles Trapezoid Height
In the isosceles trapezoid ABCD, the base length is a = 10cm, c = 6cm, and the arm's length is 4cm. Calculate its height—the result round to tenths. - Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm and CD = 4cm. Calculate the length of the AC diagonal. - Calculate 258
Calculate the volume and surface area of a prism with a trapezoidal base and a height of 9 cm. The base is an isosceles trapezoid with bases of lengths 3 cm and 6 cm and arms of length 2.5 cm. The height of the base is 2cm. - RR trapezoid 12
In an isosceles trapezoid ABCD, calculate the missing lengths of the sides when a=46cm, b=85cm height=84cm.
