Surface - formula
Of the formula, S = the surface of the cuboid S=2. (ab+ac+bc) express unknown c. C =?
Final Answer:

You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Collinear lines
 Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC?
Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC? - Expression unknown calculation
 The expression 2n + m = 52, please express an unknown n.
The expression 2n + m = 52, please express an unknown n. - Triangle ABC v2
 The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x.
The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x. - Angles
 In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β?
In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β? - Trapezoid angle calculation
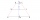 In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle.
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Bisector 2
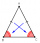 ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Quadrilateral construction
 Construct a quadrilateral ABCD with dimensions AB, BC, AC, BD, and angle d = CDA.
Construct a quadrilateral ABCD with dimensions AB, BC, AC, BD, and angle d = CDA.
