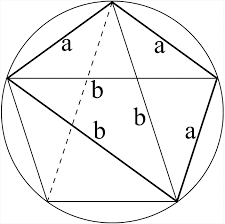
Five-gon
Calculate the side a, the circumference, and the area of the regular 5-angle if Rop = 6cm.
Correct answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Pentagon
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm. - Circumscribed 22713
Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm. - Circumference parallelogram
Calculate the circumference and area of the parallelogram ABCD if side a = 72 cm, height v = 4.3 cm, and second side b = 6 cm. - Pentagonal pyramid
Calculate the volume of a regular 5-side (pentaprism) pyramid ABCDEV; if |AB| = 7.7 cm and a plane ABV, ABC has angle 37 degrees.
- Circumference 46801
Calculate side b and the height of the trapezoid if a = 5.1cm; c = 6.8cm; d = 4.7cm; circumference is 21cm, and the area is 17.85 cm². - Circumference of a polygon
Calculate the length of the side and the regular 13-gon if you have given its circumference o = 771. - Trapezoid - sides
Calculate the unknown side and the area of the ABCD trapezoid if you know: side a = 7.5 side b = 3.6 side d = 4.4 height v = 3.4 circumference o = 19 c =? S =?
