Päťuholník
Vypočítajte stranu a, obvod a obsah pravidelného 5-uholníka, ak Rop=6cm.
Správna odpoveď:
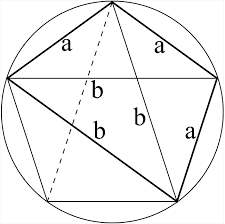
Tipy na súvisiace online kalkulačky
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Dekanon
Vypočítajte obvod a obsah pravidelného 10 uholníka ak polomer opísanej kružnice r = 20 cm. - Obvod 48
Obvod pravidelného osemuholníka je 8u + 16 cm. Vypočítajte stranu, ak u = 0,5 cm. - 12 uholník
Vypočítajte obsah pravidelného 12 uholníka, ak je jeho strana a = 12 cm. - Pravidelného 4670
Vypočítaj dĺžku strany a pravidelného 20-uholníka, ak máš daný jeho obvod o=635.
- Lichobežník 29
Vypočítajte chýbajúcu stranu a obsah lichobežníka ABCD, ak viete: a=7,5 b=3,6 d=4,4 v=3,4 o=19 c=? S=? - Rovnobežník - obvod
Vypočítajte chýbajúcich stranu rovnobežníka, ak poznáte jej obvod a jednu stranu: a) o = 7,2 cm; b = 1,8 cm b) o = 5,4 cm; a = 1,9 cm - Pravidelný 6 uholník
Pravidelný 6-uholník, ktorého strana je 5 cm. Vypočítajte jeho obsah. Porovnajte koľko viac cm² (centimetrov štvorcových) má kruh do ktorého je vpísaný tento 6-uholník.
