Proportion 20443
On line AB, 15 cm long, point C lies 4 cm from point A. In what proportion does this point divide the line AB?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Identical 8831
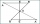In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P - Chord BC
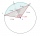A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Lie/do not lie
The rule f(x) = -x-10 gives the function. Find whether point C[5; -15] lies on this function. Solve graphically or numerically and give reasons for your answer. - triangle 5420
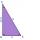Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl
- Construct diagonals
The point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of the rect - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Two chords
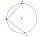There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure.
