Circle
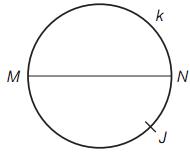
The circle k with diameter |MN| = 61. Point J lies on the circle k. Line |MJ|=22. Calculate the length of a segment JN.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- MO Z8–I–6 2018
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Chord BC
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Two points
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN.
- Square ABCD
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4]. - Proportion 20443
On line AB, 15 cm long, point C lies 4 cm from point A. In what proportion does this point divide the line AB? - Length 20353
The given line is MN with a length of 11 cm. Change its length in the ratio: a) k = 2:1 b) k = 1:2 c) k = 17:11 d) k = 22:33
