Trapezoid
The area of a trapezoid is 135 cm2. The sides a, c, and height h are in a ratio of 6:4:3. How long are sides a, c, and height h? Perform calculation.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetrybasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- What is
What is the circumference of an isosceles trapezoid with an area of 106.75 cm²? The lengths of the sides are in the ratio of 1:3:2:1, and the bases are 6.1 cm apart. - Trapezium
The area of trapezium is 35 cm². Find its height if the bases are 6 cm and 8 cm long. - The sides 2
The sides of a trapezoid are in the ratio 2:5:8:5. The trapezoid's area is 245. Find the height and the perimeter of the trapezoid. - Trapezoid height calculation
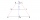The trapezoid area is 40.8 cm². Calculate the height of the trapezoid if the base is 5.5 cm long and 4.7 cm long. - Pillar - bricks
A brick pillar has the shape of a four-sided prism with an isosceles trapezoid base with parallel sides a = 55 cm and c = 33 cm, leg b = 33 cm, and trapezoid height vₐ = 32.1 cm. The pillar is 1.9 m high. How many bricks were used to build it if one brick - Centimeters - trapezoid
The area of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Find the height of the trapezoid in centimeters. - Trapezoid area calculation
The LICH isosceles trapezoid has 5.2 cm long arms and its bases are 7.6 cm and 3.6 cm long. Find the area of the LICH trapezoid.
