Right angle
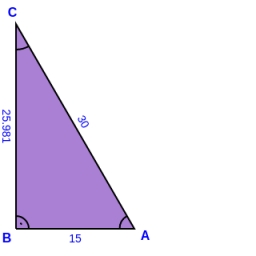
In a right triangle ABC with a right angle at the apex C, we know the side length AB = 24 cm and the angle at the vertex B = 71°. Calculate the length of the legs of the triangle.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Maturitný - RR - base
In an isosceles triangle ABC with base AB, ∠BAC = 20° and AB = 4. The angle bisector from vertex B intersects side AC at point P. Calculate the length of segment AP. Give the result to two decimal places. - Triangle area and angle
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the vertex A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 . - Z7-I-5 MO 2017
Prokop constructed a triangle ABC whose interior angle at vertex A was greater than 60° and whose interior angle at vertex B was less than 60°. Juraj drew, in the half-plane determined by line AB and point C, a point D such that triangle ABD was equilater - Triangle ABC
Right triangle ABC with right angle at the C, |BC|=19, |AB|=26. Calculate the height of the triangle hAB to the side AB. - What is 19
What is the length of the hypotenuse c of right triangle ABC if the angle α at vertex A is 30° and leg a = 3 cm? - Triangle angle ratio
In the right-angled triangle ABC (the right angle at vertex C), the angle ratio is α : β = 5 : 3. Calculate the sizes of these angles and convert them to degrees and minutes (e.g., 45°20') - 3 positive charges
Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1 m. What is the electric field strength at the center S of side BC, i.e., what force would act on a po
