Centre of mass
The vertices of triangle ABC are from the line p distances 3 cm, 4 cm, and 8 cm. Calculate the distance from the center of gravity of the triangle to line p.
Correct answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - Perimeter - general
 Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side.
Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side. - Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - The triangle 6
 The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning. - EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
- X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Mast angles and height
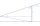 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Trigonometric fx
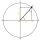 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Using 4
 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
- A triangular
 A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides?
A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides? - Panting
 If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.?
If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.? - Three angles
 The three angles of a triangle are (3x-2)°, (4x+5)°, and (2x-3)°, then find the angles.
The three angles of a triangle are (3x-2)°, (4x+5)°, and (2x-3)°, then find the angles.
