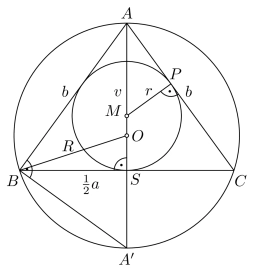
Sides ratio and angles
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Calculate 83261
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 - The right triangle
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles. - Triangle sides to angles
The triangle ABC has side lengths a = 14 cm, b = 20 cm, c = 7.5 cm. Find the sizes of the angles and the area of this triangle. - Millimeters 4811
Construct a triangle ABC if you know the lengths of its sides c = 5 cm, a = 4 cm and angle ABC is 60°. Measure the length of side b in millimeters. Side length b is: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm
- Draw SSA triangle
Draw a triangle ABC if you know: alpha = 60° side b = 4 cm side a = 10 cm - Right-angled 81019
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Construction
Construct the triangle ABC if you know: the size of the side AC is 6 cm, the size of the angle ACB is 60°, and the distance of the center of gravity T from the vertex A is 4 cm. (Sketch, analysis, notation of construction, construction)
