Těžiště
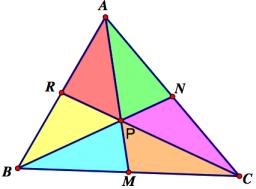
Vrcholy trojúhelníku ABC mají od přímky p po řadě vzdálenost 3 cm, 4 cm a 8 cm. Urči vzdálenost těžiště trojúhelníku od přímky p.
Správná odpověď:
Zobrazuji 1 komentář:
Ivo
souřadnice těžiště trojúhelníku jsou aritmetickým průměrem souřadnic jednotlivých bodů. souřadnice x, y těžiště jsou vzdálenosti těžiště od souřadnicových os y, x, Což jsou takové jenom přimknout. Proto i když známe vzdálenosti od obecně umístěné přímky, bude arit. průměr vzdáleností vrcholů od přímky vzdálenosti těžiště od této přímky
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem aritmetického průměru?
Hledáte statistickou kalkulačku?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Hledáte statistickou kalkulačku?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Těžnice - vzdálenosti
Těžnice t na stranu b (tb) v trojúhelníku ABC má délku 12 cm. a, jaká je vzdálenost těžiště T od vrcholu B b, urči vzálenost T od strany b. - Těžiště
Sestroj trojúhelník ABC, pokud je dané: velikost strany AC je 6 cm, velikost úhlu ACB je 60° a vzdálenost těžiště T od vrcholu A je 4 cm. (Náčrt, rozbor, zápis konstrukce, konstrukce) - V rovnoramenném
V rovnoramenném trojúhelníku ABC je těžiště T vzdáleno 2 cm od základny AB. Střední příčka rovnoběžná se stranou AB měří 4cm. Jaký obsah má trojúhelník ABC? - Trojúhelníku 6002
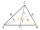V trojúhelníku ABC je dána strana c=5cm a těžnice ta=6cm, tb=4,5cm. Vypočítá obvod trojúhelníku ABT (T= těžiště). - Těžiště
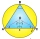Těžiště trojúhelníku ABC je v bodě (3,3,3). Pokud jsou souřadnice bodů A a B (3, –5, 7) a (–1, 7, – 6), najděte souřadnice bodu C. @@ - Těžiště
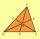V trojúhelníku ABC leží bod D[1,-2,6], který je středem strany |BC| a bod G, který je těžištěm trojúhelníku G[8,1,-3]. Najděte souřadnice vrcholu A[x,y,z]. - Příčka v trojúhelníku
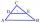V trojúhelníku ABC se stranou/AB/ = 24 cm je sestrojena příčka/DE/ = 18 cm rovnoběžná se stranou AB ve vzdálenosti 1 cm od AB. Vypočítejte výšku trojúhelníku ABC na stranu AB.
