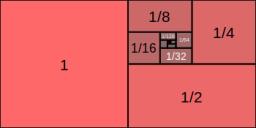
Gp - 80
The sum of the first four members of a geometric progression is 80. Find it if we know that the fourth member is nine times greater than the second.
Your answer:
Your answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticGrade of the word problem
Related math problems and questions:
- Determination of a sequence
A sequence is given whose first three members are a1= 70, a2=64, a3=58. 1, decide whether it is an arithmetic or a geometric sequence and accordingly determine the value of d or q. 2, determine the value of the fifteenth member of the sequence. 3, determi - Sequences AP + GP
The three numbers that make up the arithmetic sequence have the sum of 30. If we subtract from the first 5, the second 4, and keep the third, we get the geometric series. Find AP and GP members. - Geometric progressiob
If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms. - Geometric progression members We get three consecutive GP members if we subtract the same number from 33, 45, and 63. Determine this GP and calculate its fifth member.
- The sum 27
The sum of a geometric progression's second and third terms is six times the fourth term. Find the two possible values of the common ratio. - Three members GP
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers. - Geometric progression
Determine the fourth GP member if q = 4 and a1 + a3 = 5.44
