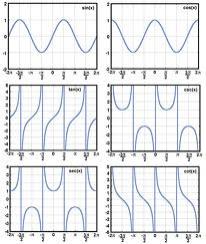
Trigonometric functions
In the right triangle is:
tg α=24
Find the value of s and k:
sin α=20s
cos α=20k
tg α=24
Find the value of s and k:
sin α=20s
cos α=20k
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsnumbersgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Sin cos tan
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - Q-Exam
If tg α = 8.6, Calculating sin α, cos α, cotg α . - A right
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Moivre 2
Find the cube roots of 125(cos 288° + i sin 288°). - Cotangent
If the angle α is acute, and cotan α = 1/3. Determine the value of sin α, cos α, and tan α. - Trigonometry
If you know that cos(γ) = sin (806°), what is the angle γ? - Sin cos tan
In triangle ABC, right-angled at B. Sides/AB/=7cm, /BC/=5cm, /AC/=8.6cm. Find two decimal places. A. Sine C B. Cosine C C. Tangent C.
