Q-Exam
If tg α = 8.6, Calculating sin α, cos α, cotg α .
Correct answer:
Tips for related online calculators
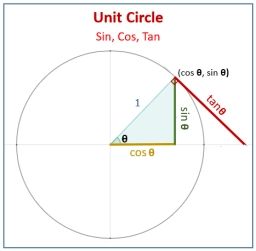
The Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Trigonometric functions
In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20) - Trigonometric formula
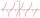Determine the value of the function tg x (tangent) when cotan x = -0.8 (cotg or cotangent); x holds in the second quadrant) - Trigonometry
If you know that cos(γ) = sin (806°), what is the angle γ? - Cotangent
If the angle α is acute, and cotan α = 1/3. Determine the value of sin α, cos α, and tan α.
- Sin cos tan
In triangle ABC, right-angled at B. Sides/AB/=7cm, /BC/=5cm, /AC/=8.6cm. Find two decimal places. A. Sine C B. Cosine C C. Tangent C. - Sin cos tan
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - Substitution method
Solve a goniometric equation: sin4 θ - 1/cos² θ=cos² θ - 2
