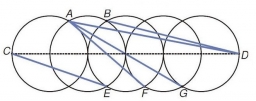
Five circles
On the line segment CD = 6 there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - triangle 5420
Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Construct 30121
Point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of rectangle AB - Trapezium ABCD
The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60 - Angle of two lines
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Three lines
At 6 AM, three bus lines depart from the station. The first line has an interval of 24 minutes. The second line has an interval of 15 minutes. The third line runs at regular intervals of more than 1 minute. The third line runs at the same time as the firs - Trapezoid ABCD
ABDC is a trapezoid in which AB and CD are parallel sides measuring 6 and 9, respectively. Angles ABC and BCD are both right angles. Find the length of segment BD. - Deviation of the lines
Find the deviation of the lines AG, BH in the ABCDEFGH box-cuboid, if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Intervals 3487
The four teams left the terminal together at 5:00 in the morning. Line A runs at 15-minute intervals, line B at 6-minute intervals, line C at 20-minute intervals, and line D at 8-minute intervals. What time did all four lines leave the terminal together a - Individual 6270
Divide three lines with lengths of 12 cm, 24 cm, and 64 cm into equally long and, at the same time, the most extended possible parts. How long will the individual parts be, and how many will there be? - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Construction 32971
There is any circle k that does not have a marked center. Use a suitable construction to find the center of the circle k. Try on two different circles. - Suppose
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not? - Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Diagonal BD
Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42°
