Antenna mast
The antenna mast is 26 meters high. It is fixed by four steel cables suspended 1.6 meters below the highest point of the mast and anchored to the ground at the vertices of a square with a side length of 14 meters. The mast is erected in the center of this square. Calculate the total length of the ropes if 1.5 m is added to secure each one.
Final Answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsGrade of the word problem
Related math problems and questions:
- Mast rope anchoring
 The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed?
The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed? - Column rope length
 The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po
The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po - Transmitter rope
 A television transmitter 108 m high is anchored at 2/3 of its height (from the ground) by three ropes of equal length. How many meters of rope are needed for anchoring if it is embedded at a distance of 54 m from the foot of the mast, and we count 10% of
A television transmitter 108 m high is anchored at 2/3 of its height (from the ground) by three ropes of equal length. How many meters of rope are needed for anchoring if it is embedded at a distance of 54 m from the foot of the mast, and we count 10% of - A transmitter tower
 A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u
A transmitter tower is 80 meters high and is stabilized to the ground by 4 steel cables anchored in the ground 60 meters from the base of the tower. Calculate how many meters of steel cable were needed to stabilize the transmitter tower. The steel cable u - Sailboat
 The 20 m long sailboat has an 8 m high mast in the middle of the deck. The top of the mast is fixed to the bow and stern with a steel cable. Determine how much cable is needed to secure the mast and what angle the cable will make with the ship's deck.
The 20 m long sailboat has an 8 m high mast in the middle of the deck. The top of the mast is fixed to the bow and stern with a steel cable. Determine how much cable is needed to secure the mast and what angle the cable will make with the ship's deck. - Rotatable tower
 The rotatable tower situated in the city center has the ground shape of a regular polygon. If the tower is rotated by 18° around its centerpiece, it looks from the side same. Your task is to calculate at least how many vertices can have a ground plan view
The rotatable tower situated in the city center has the ground shape of a regular polygon. If the tower is rotated by 18° around its centerpiece, it looks from the side same. Your task is to calculate at least how many vertices can have a ground plan view - A radio antenna
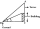 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
