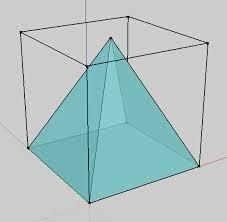
Pyramid in cube

In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid.

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebra

rearrange variables

arithmetic

square root

solid geometry

cube
pyramid
surface area

planimetry

Pythagorean theorem
right triangle
area of a shape
triangle

Units of physical quantities

volume

Grade of the word problem

practice for 13 year olds
practice for 14 year olds
high school

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

Block cube surface
We get a block if we stack two cubes with an edge of 1 dm. What is the difference between the surfaces of this block and the cube?
Pyramid surface volume
Calculate the surface area and volume of a regular quadrilateral pyramid if the edge of the lower base is 18 cm and the edge of the upper base is 15 cm. The wall height is 9 cm.
Cube surface
A large cube with an edge of length 3 is given. One small cube with a volume 27 times smaller than the volume of the large cube is glued to each of its faces. All the small cubes touch the big ones through the wall. What surface does this body have?
The cube
The cube has a surface area of 216 dm². Calculate: a) the area of one wall, b) edge length, c) cube volume.
Cube measurements
The surface area of one cube wall is 2500 square millimeters. Determine the cube's surface, the length of its edge, and its volume.
Tower
Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have?
Cube edge ratio
The lengths of the edges of two cubes are in the ratio 1:2, determine: a) the ratio of the area of the wall of the smaller cube to the area of the wall of the larger cube. b) the ratio of the surface of the smaller cube to the surface of the larger cube.