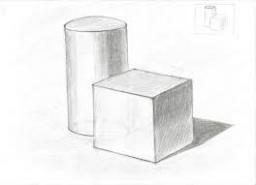
Surface area of cylinder
Determine the lateral surface of the rotary cylinder, which is a circumscribed cube with a 5 cm edge length.
Your answer:
Your answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rotary cone
The volume of the rotation of the cone is 733 cm³. The angle between the side of the cone and the base angle is 75°. Calculate the lateral surface area of this cone. - Lateral surface area
The ratio of the area of the base of the rotary cone to its lateral surface area is 3:5. Calculate the surface and volume of the cone if its height v = 4 cm. - Cube edge
Determine the edge length of a cube whose surface area is 37.5 cm². - Cylinder in a Cube
The cube has an edge length of 5 cm. This cube surrounds a rotating cylinder. Find the surface area of the shell and the volume of the cylinder. - Sphere area
A cube with an edge 1 m long is a circumscribed sphere (vertices of the cube lie on a sphere's surface). Find the surface area of the sphere. - Triangular pyramid
Determine the volume and surface area of a regular triangular pyramid having a base edge a=20 cm and a lateral edge b = 35 cm. - Cylinder - curved area
The curved area of the rotary cylinder is three times greater than the area of one base of this cylinder. The radius of the base of the cylinder is 10 cm. What is the surface area of the cylinder?
