Consider
Consider all square prisms with a height of 10 cm.
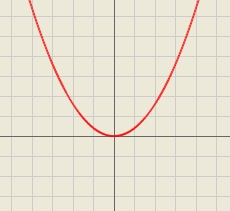
If x is the measurement of the base edge in cm, and y is the prism's volume in cm3. Graph the function
If x is the measurement of the base edge in cm, and y is the prism's volume in cm3. Graph the function
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- 3s prism
A regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm is given. Calculate the prism's volume. - Calculate 25391
The base of the prism is a square with a side of 10 cm. Its height is 20 cm. Calculate the height of a pyramid with a square base of 10 cm, which has four times the prism's volume. - Rhombus base
Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 12 cm and u2 = 15 cm. The prism height is twice the base edge length. - Calculate 26051
The base of the prism is a square with a side of 10 cm. Its height is 20 cm. Calculate the height of a pyramid with a square base of 10 cm, which has four times the prism's volume.
- Cantilevers 81937
Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm. - Prism height
What is the prism's height with the base of a right triangle of 6 cm and 9 cm? The diaphragm is 10.8 cm long. The volume of the prism is 58 cm³. Calculate its surface. - Hexagonal prism
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
