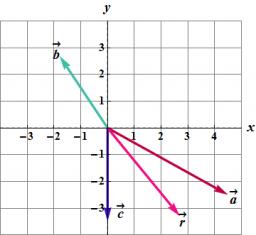
Vector 7
Given vector OA(12,16) and vector OB(4,1). Find vector AB and vector |A|.
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Displacement 55871
Assemble the two offsets, d1, and d2, shown by OA and OB oriented lines. The coordinates of the points are O = (0m, 0m), A = (3m, 3m), and B = (5m, 2m). Measure the magnitude of the resulting displacement d. - Perpendicular lines
Points A(1,2), B(4,-2) and C(3,-2) are given. Find the parametric equations of the line that: a) It passes through point C and is parallel to the line AB, b) It passes through point C and is perpendicular to line AB. - Place vector Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO.
- Distance of the parallels
Find the distance of the parallels, which equations are: x = 3-4t, y = 2 + t and x = -4t, y = 1 + t (instructions: select a point on one line and find its distance from the other line)
- The diagonals 2
The diagonals AC and BD of a rectangle ABCD intersect at a point O. If OA=4cm, find AC and BD. - Equation 2604
The given triangle is ABC: A [-3; -1] B [5; 3] C [1; 5] Write the line equation that passes through the vertex C parallel to the side AB. - Angle ASB
On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets.
