Find two
Find two consecutive natural numbers whose product is one larger than their sum. Searched numbers are expressed by a fraction whose numerator is the difference between these numbers, and the denominator is their sum.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebrabasic operations and conceptsnumbersGrade of the word problem
Related math problems and questions:
- Denominator numerator difference
The denominator is 1628 larger, than the denominator. What is the difference? - Numerators and denominators 2
A fraction becomes 2 when 1 is added to both the numerator and denominator and it becomes 3 when 1 is subtracted from both numerator and denominator. Find the difference of numerator and denominator. - Adjust numerators
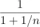If the numerator of a fraction is increased by 2 and the denominator by 1, it becomes 5/8. If the numerator and the denominator of the same fraction are each increased by 1, the fraction becomes 1/2. Find the fraction. - Division by zero
Fraction 5 by 2. if three is added to the numerator and two is subtracted from the denominator, then the new fraction is: - A farm 6
A farm has 20 animals. There are four chickens. What fraction of the animals are chickens? Express your answer as a fraction in the simplest form. - Denominator 2
The denominator of a fraction is five, and the numerator is 7. Write the fraction. - Fraction
Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator.
