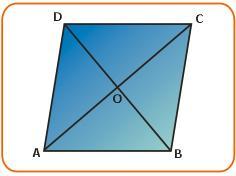
Rhombus
Internal angles of a rhombus are in ratio 2:5.
How many times is the shorter diagonal longer than the side of the rhombus?
How many times is the shorter diagonal longer than the side of the rhombus?
Final Answer:
Tips for related online calculators
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- One of
One of the internal angles of the rhombus is 120°, and the shorter diagonal is 3.4 meters long. Find the perimeter of the rhombus. - Rhombus 47
A rhombus has a side length of 5 m and a longer diagonal length of 8 m. What is the length of the shorter diagonal of the rhombus? - Determine 83081
A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid. - Diagonals
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°. - Diagonal
Can it be a diagonal diamond twice longer than its side? - Sides of triangle
Triangle has a circumference of 42 cm. Side a is two times shorter than side b, and side c is 2 cm longer than side a. Find the sizes of the sides of a triangle. - The area
The area of a rhombus is 143 m². If the longer diagonal is 26 m, find the shorter diagonal in inches named d1.
