Cancel fractions
Compress the expression of factorial:
(n+6)!/(n+4)!-n!/(n-2)!
(n+6)!/(n+4)!-n!/(n-2)!
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Would you like to compute the count of combinations?
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Five couples
 In how many ways can 5 couples arrange themselves in a row if they stay together?
In how many ways can 5 couples arrange themselves in a row if they stay together? - SKMO
 Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product.
Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product. - Gradually 67284
 Petra borrowed four books from the library at the beginning of the summer holidays. How many orders in which she could gradually read them?
Petra borrowed four books from the library at the beginning of the summer holidays. How many orders in which she could gradually read them? - Word OPTICAL
 Find the number of possible different arrangements of the letters of the word OPTICAL such that the vowels would always be together.
Find the number of possible different arrangements of the letters of the word OPTICAL such that the vowels would always be together.
- Triangle from sticks
 Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks?
Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks? - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - The flag
 The flag should consist of 3 different colored stripes - available colors: white, red, blue, green, and yellow. Specify: A) number of all flags B) number of flags with a blue stripe C) number of flags with a blue stripe in the middle D) the number of flag
The flag should consist of 3 different colored stripes - available colors: white, red, blue, green, and yellow. Specify: A) number of all flags B) number of flags with a blue stripe C) number of flags with a blue stripe in the middle D) the number of flag - How many 13
 How many ways can X³ y⁴ z³ be written without an exponent?
How many ways can X³ y⁴ z³ be written without an exponent? - A department
 There are seven women and five men in a department. a) how many ways can a committee of 3 people be selected? b) how many ways can a committee of 2 men and one woman be selected? c) how many ways can a committee of at least two women be selected (3 people
There are seven women and five men in a department. a) how many ways can a committee of 3 people be selected? b) how many ways can a committee of 2 men and one woman be selected? c) how many ways can a committee of at least two women be selected (3 people
- Factorial cancellation
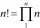 Cancel the expression with factorials: 12! x 2 x 7! / 6 x 10! 8!
Cancel the expression with factorials: 12! x 2 x 7! / 6 x 10! 8! - Permutations with repetitions
 How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the
How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the - Cups on the shelf
 We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side?
We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side? - Round table
 Eight people are sitting at a round table. In how many ways can they be seated around the table?
Eight people are sitting at a round table. In how many ways can they be seated around the table? - Wedding guests
 Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs.
Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs.
- You have
 You have four reindeer, and you want to have 3 fly your sleigh. You always have your reindeer fly in a single-file line. How many different ways can you arrange your reindeer?
You have four reindeer, and you want to have 3 fly your sleigh. You always have your reindeer fly in a single-file line. How many different ways can you arrange your reindeer? - Coffe cups
 We have 4 cups with four different patterns. How many possible combinations can we create from 4 cups?
We have 4 cups with four different patterns. How many possible combinations can we create from 4 cups? - Wagons
 We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many di
We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many di
