Count of triangles
On each side of an ABCD square is 10 internal points.
Determine the number of triangles with vertices at these points.
Determine the number of triangles with vertices at these points.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- In an
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - N points on the side
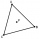An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides. - Combi-triangle
Each square side is marked 10 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square? - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Construct 30121
Point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of rectangle AB - Different 42191
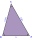How many different triangles with vertices formed by points A, B, C, D, E, and F can we create? - Square 2
Points D[10,-8] and B[4,5] are opposed vertices of the square ABCD. Calculate the area of the square ABCD. - Coordinates of the intersection of the diagonals
In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle. A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle. - Right-angled 66344
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm². - Surveyors
Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other? - Respectively 81293
The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help... - Rectangle - parallelogram
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Circle and square
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Hexagon - MO
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and is true |DJ| - Similarity coefficient
In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other. - Similarity of squares
The ratio of the similarity of the squares ABCD and KLMN is 2.5. Square KLMN area is greater than an area of a square ABCD with side a: ... - Respectively 80982
The vertices of the square ABCD are joined by the broken line DEFGHB. The smaller angles at the vertices E, F, G, and H are right angles, and the line segments DE, EF, FG, GH, and HB measure 6 cm, 4 cm, 4 cm, 1 cm, and 2 cm, respectively. Determine the ar
