Trapezoid Billboard Area Gain
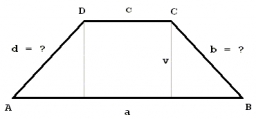
The advertising agency invented a new shape for billboards to attract attention - a trapezoid. How much more m2 of area did they gain if the size of the classic billboard is 5.1x2.4 m and the dimensions of the trapezoidal billboard are 4.2 and 6 m bases and 2.4 m height?
Your answer:
Your answer:
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Garden exchange
The garden has a rectangular trapezoid shape, the bases of which have dimensions of 60 m and 30 m and a vertical arm of 40 m. The owner exchanged this garden for a parallelogram, which is 7/9 of the area of a trapezoidal garden. What is the size of the ne - Pyramid Volume Trapezoid Base
Calculate the volume of a 1.3 dm high pyramid with a trapezoidal base. The bases are 2.3 dm and 1.6 dm long, and the pyramid's height is 1.8 dm. - Roof tiles
The roof has a trapezoidal shape with bases of 15 m and 10 m, and its height is 4 meters. If a one-meter square should be used for eight tiles, how many tiles will be needed? - Park tree
How many trees are planted in a trapezoidal park with bases of 35.7 m, 13.3 m, arms of 20 m and 22 m, and a height of 19 m if one tree needs nine m²? - Orchard
The route passes the trapezoidal orchard perpendicular to the parallel sides. It is 80 cm wide. The lengths of the bases are in the ratio 5:3. The length of the longer base to the size of the path is in the ratio of 5:6. How many square meters occupy the - Trapezoidal prism surface
The prism with a trapezoidal base has the dimensions of the base a = 10 cm, b = d = 5 cm, c = 6 cm, the trapezoid height is 4.6 cm, and the height of the prism is 30 cm. Calculate its surface. - Dimensions of the trapezoid
One of the trapezoid bases is one-fifth larger than its height, and the second base is 1 cm larger than its height. Find the dimensions of the trapezoid if its area is 115 cm2
