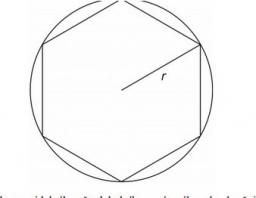
Hexagon
There is a regular hexagon ABCDEF. If the area of the triangle ABC is 10, what is the area of the hexagon ABCDEF?
I do not know how to solve it simply....
I do not know how to solve it simply....
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- similarity of triangles
- arithmetic
- square root
- rounding
- planimetrics
- right triangle
- polygon
- area of a shape
- triangle
- basic functions
- reason
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Determine 69304
Determine the size of the ACF angle in the regular ABCDEF hexagon. - Hexagon ABCDEF
In the regular hexagon ABCDEF, the diagonal AE has a length of 8cm. Calculate the circumference and the hexagon area. - Coordinates hexagon
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - Irregular hexagon
There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and 193. What is its area?
- Hexagon
Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter? - The perimeter
The perimeter of equilateral △PQR is 12. The perimeter of the regular hexagon STUVWX is also 12. What is the ratio of the area of △PQR to STUVWX? - Inscribed 7018
The dragon has the shape of a regular hexagon inscribed in a circle with a radius of 20 cm. What is the area of the dragon?
