Two doctors
Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient.
Correct answer:
Showing 1 comment:
Math student
To calculate the probability of proper diagnosis if both doctors diagnose the patient, we can use the multiplication rule of probability:
P(A and B) = P(A) * P(B)
where P(A and B) is the probability that both doctors A and B diagnose the patient correctly, P(A) is the probability that doctor A diagnoses the patient correctly, and P(B) is the probability that doctor B diagnoses the patient correctly.
We are given that the probability of correct diagnosis by doctor A is 0.93 (or 93%) and the probability of correct diagnosis by doctor B is 0.79 (or 79%). Therefore:
P(A) = 0.93
P(B) = 0.79
To find the probability that both doctors diagnose the patient correctly, we multiply the probabilities:
P(A and B) = P(A) * P(B) = 0.93 * 0.79 = 0.7347
Therefore, the probability of proper diagnosis if both doctors diagnose the patient is approximately 0.7347 or 73.47%.
P(A and B) = P(A) * P(B)
where P(A and B) is the probability that both doctors A and B diagnose the patient correctly, P(A) is the probability that doctor A diagnoses the patient correctly, and P(B) is the probability that doctor B diagnoses the patient correctly.
We are given that the probability of correct diagnosis by doctor A is 0.93 (or 93%) and the probability of correct diagnosis by doctor B is 0.79 (or 79%). Therefore:
P(A) = 0.93
P(B) = 0.79
To find the probability that both doctors diagnose the patient correctly, we multiply the probabilities:
P(A and B) = P(A) * P(B) = 0.93 * 0.79 = 0.7347
Therefore, the probability of proper diagnosis if both doctors diagnose the patient is approximately 0.7347 or 73.47%.
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Would you like to compute the count of combinations?
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Probability 86
At a business conference, there were ten social workers, 16 doctors, five lawyers, and two journalists. If a person is picked at random from the entire group, what is the probability: a) to be a lawyer b) to be a doctor. - Doctors
The drug successfully treats 90% of cases. Calculate the probability that it will cure at least 18 patients out of 20. - Doctors
In the city operates 196 doctors. The city has 134456 citizens. How many citizens are per doctor? - Effectiveness 80811
According to clinical studies, the effectiveness of the drug is 90%. The doctor prescribed the medicine to eight patients. What is the probability that the drug will be effective in all these patients? - Successfully 19843
The drug successfully treats the disease in 96% of cases. Your doctor will treat 50 patients with this medicine. What number of cures is most likely? - Std-deviation
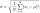Calculate standard deviation for file: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90 - Probability 30271
The probability of an adverse drug reaction is 2.1%. How many people need to be prescribed for one patient to experience side effects with a chance of 90%? - Probability of malaria
A survey carried out at a certain hospital indicates that the probability that a patient testing positive for malaria is 0.6. What is the probability that two patients were selected at random (i) one is negative while the other tested positive (i) both pa - An aircraft
An aircraft manufacturing company has submitted bids on two separate airline contracts, A and B. The company feels it has a 70% chance of winning contract A and a 25% chance of winning contract B. Furthermore, it believes that winning contract A is indepe - Mastering
The student masters the subject matter for the exam in Czech to 98%, from Math to 86%, and from Economics to 71%. What is the probability that he will fail in Math and that others will succeed? - Content 4774
There is 50 mg of Dolsin in 1 ampoule with a content of 1 ml. The patient should receive 70mg. How many ml will I draw from the second ampoule into the syringe? - The average 7
The average lifespan for cricket is 90 days, with a standard deviation of 13 days. If we assume that the lifespan of cricket is normally distributed, a. What is the probability a randomly selected cricket has a lifespan of fewer than 75 days? b. What is t - Nathan
Nathan is playing a trivia game. Each correct answer is worth 2 ½ points, and each incorrect answer is worth -¼ points. If he gets 35 questions correct and 32 questions incorrect, how many points does he have? A. 87.5 B. 79.5 C. 75 D. 8 - Matilda
Matilda measures the perimeter of her bedroom to determine how many feet of the border she needs to go around the tops of the walls. Two walls are each 96 inches long, and two walls are each 3 yards long. She pays $30 for a border that costs $1 per foot. - Probability 81677
The probability that a plant will grow from a seed is 75%. What is the probability that 5 plants will grow if we assemble 6 seeds? - Boys and girls
There are 11 boys and 18 girls in the classroom. Three pupils will answer. What is the probability that two boys will be among them? - Probability 7154
82% of football players, and 26% are hockey players at school. What is the probability that: A) I'm not a hockey player B) I know both sports C) I know one sport
