Algebra - math word problems - page 52 of 304
Number of problems found: 6080
- Lcm to eliminate y
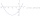 Identify the least common multiple that would eliminate the y-variable. 6x - 5y = -4 4x + 2y = 28
Identify the least common multiple that would eliminate the y-variable. 6x - 5y = -4 4x + 2y = 28 - Six hens
 Six hens weigh 3 kg more than three geese and 7 kg less than five geese. How much does a hen weigh, and how many geese?
Six hens weigh 3 kg more than three geese and 7 kg less than five geese. How much does a hen weigh, and how many geese? - Second 43001
 On the first day, Lenka read half of the book. On the second day, half of the rest, and on the third day, she read 35 pages and read the book. How many pages did the book have?
On the first day, Lenka read half of the book. On the second day, half of the rest, and on the third day, she read 35 pages and read the book. How many pages did the book have? - Smallest 42541
 Write the number 937289 larger than the smallest 6-digit odd number.
Write the number 937289 larger than the smallest 6-digit odd number. - Proportion 42381
 If you divide the unknown number x by the number (-4) and divide the resulting proportion by the number (-3), you get -2. What is x?
If you divide the unknown number x by the number (-4) and divide the resulting proportion by the number (-3), you get -2. What is x? - Missing digit
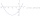 If 4x/6x + 5/17 = 1, what digit does the x represents
If 4x/6x + 5/17 = 1, what digit does the x represents - Email hoard
 Kendrick received 24 fewer e-mails on Friday than he did on Thursday. If he received a total of 126 e-mails on those two days, how many did he get each day?
Kendrick received 24 fewer e-mails on Friday than he did on Thursday. If he received a total of 126 e-mails on those two days, how many did he get each day? - Functions 42201
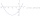 Y = x² + 4x-2 Quadratic functions Calculate and graph.
Y = x² + 4x-2 Quadratic functions Calculate and graph. - One-fifth 42071
 One-fifth of twice the number t is one.
One-fifth of twice the number t is one. - Apartment building
 Two hundred eight people live in the apartment building. There are as many women as there are men, but there are 22 more children than women. How many adults live in an apartment building?
Two hundred eight people live in the apartment building. There are as many women as there are men, but there are 22 more children than women. How many adults live in an apartment building? - Family age
 Kubo is 14 years old and has a one-year-old sister, Nina, and a four-year-old brother, Sam. In how many years will Nina and Sam be as old as Kubo?
Kubo is 14 years old and has a one-year-old sister, Nina, and a four-year-old brother, Sam. In how many years will Nina and Sam be as old as Kubo? - Pilgrimage 41951
 Pavel spent CZK 315 on the pilgrimage in three days, doubling his spending every following day. How much CZK did he pay on the first day?
Pavel spent CZK 315 on the pilgrimage in three days, doubling his spending every following day. How much CZK did he pay on the first day? - Happy marriage
 Jan and Marienka have been in a happy marriage for several years. Jan's age is written in the same numbers as Marienka's, only in reverse order. Their ages differ by just a fifth of Marienka's. Jan is older. How old is Jan, and how many is Marienka?
Jan and Marienka have been in a happy marriage for several years. Jan's age is written in the same numbers as Marienka's, only in reverse order. Their ages differ by just a fifth of Marienka's. Jan is older. How old is Jan, and how many is Marienka? - Miguel
 Miguel and Kat are reading the same book. Miguel reads the book three times as many pages as Kat. Together, they read 48 pages. Write an equation that we can use to find how many pages Kat read.
Miguel and Kat are reading the same book. Miguel reads the book three times as many pages as Kat. Together, they read 48 pages. Write an equation that we can use to find how many pages Kat read. - Solutions 41771
 There were 32 toys on the toy store shelf. We know that there were 19 cars with these toys. We also know that 18 of these toys were made of wood. How many wooden cars were on the shelf? Find at least two solutions.
There were 32 toys on the toy store shelf. We know that there were 19 cars with these toys. We also know that 18 of these toys were made of wood. How many wooden cars were on the shelf? Find at least two solutions. - Giraffe 2
 The lifespan of a guinea pig is six years less than that of a giraffe. The lifespan of a tiger is four times that of a guinea pig. If the total lifespan of the animals is 30 years, calculate the longevity of the giraffe.
The lifespan of a guinea pig is six years less than that of a giraffe. The lifespan of a tiger is four times that of a guinea pig. If the total lifespan of the animals is 30 years, calculate the longevity of the giraffe. - Guilders 40991
 The price for 1 acre of good land is 300 gold coins, and the price for 7 acres of bad land is 500 gold. The buyer bought a total of 100 acres for 10,000 guilders. How many acres of good and how many acres of bad land did he buy?
The price for 1 acre of good land is 300 gold coins, and the price for 7 acres of bad land is 500 gold. The buyer bought a total of 100 acres for 10,000 guilders. How many acres of good and how many acres of bad land did he buy? - There 5
 There were 429 people at the play. Admission was 50 pesos each for adults and 35 pesos each for children. The receipts were 17265 pesos. How many adults and how many children attended?
There were 429 people at the play. Admission was 50 pesos each for adults and 35 pesos each for children. The receipts were 17265 pesos. How many adults and how many children attended? - The cost
 The amusement ticket costs 250 pesos for children and 500 pesos for adults. On a certain day, attendance at the park is 2,000, and the total revenue is 750000 pesos. How many children and how many adults bought the tickets?
The amusement ticket costs 250 pesos for children and 500 pesos for adults. On a certain day, attendance at the park is 2,000, and the total revenue is 750000 pesos. How many children and how many adults bought the tickets? - Two markers
 Two markers and one eraser cost 35 pesos, and three markers and four erasers cost 65 pesos. Find the cost of a marker and an eraser.
Two markers and one eraser cost 35 pesos, and three markers and four erasers cost 65 pesos. Find the cost of a marker and an eraser.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
