Angle practice problems - page 25 of 64
Number of problems found: 1262
- Depth angles
 At the top of the mountain stands a castle with a tower 30 meters high. We see the crossroad at a depth angle of 32°50' and the heel at 30°10' from the top of the tower. How high is the top of the mountain above the crossroad?
At the top of the mountain stands a castle with a tower 30 meters high. We see the crossroad at a depth angle of 32°50' and the heel at 30°10' from the top of the tower. How high is the top of the mountain above the crossroad? - Steeple
 The church tower is seen from the road at an angle of 52°. When we zoom out to 29 meters away, it can be seen at an angle of 21°. How high is it?
The church tower is seen from the road at an angle of 52°. When we zoom out to 29 meters away, it can be seen at an angle of 21°. How high is it? - Third roots
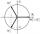 Determine the sum of the three complex third roots of the number 64 .
Determine the sum of the three complex third roots of the number 64 . - Inclination of a hill
 A skier starts down a hill of length l and an angle of inclination of 10˚. It then moves to a horizontal section of the track, which travels the same length l until it stops. Determine the coefficient of sliding friction between the skis and the snow.
A skier starts down a hill of length l and an angle of inclination of 10˚. It then moves to a horizontal section of the track, which travels the same length l until it stops. Determine the coefficient of sliding friction between the skis and the snow. - Medians in right triangle
 It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides?
It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides? - Roof angle
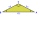 The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make? - Aircraft
 The plane flies at altitude 6300 m. At the time of the first measurement was to see the elevation angle of 21° and the second measurement of the elevation angle of 46°. Calculate the distance the plane flew between the two measurements.
The plane flies at altitude 6300 m. At the time of the first measurement was to see the elevation angle of 21° and the second measurement of the elevation angle of 46°. Calculate the distance the plane flew between the two measurements. - Elevation angle
 An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly?
An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly? - Observation 76644
 From the smaller observation tower, we see the top of the larger tower at an elevation angle of 23°, and the difference in their heights is 12 m. How far apart are the observation towers?
From the smaller observation tower, we see the top of the larger tower at an elevation angle of 23°, and the difference in their heights is 12 m. How far apart are the observation towers? - Standing 22821
 The heating plant sees the observer standing 26 m from the bottom of the chimney and seeing the top at an angle of 67 °. Thus, the chimney of the heating plant is how high?
The heating plant sees the observer standing 26 m from the bottom of the chimney and seeing the top at an angle of 67 °. Thus, the chimney of the heating plant is how high? - The isosceles
 The isosceles trapezoid ABCD has bases of 18 cm and 12 cm. The angle at apex A is 60°. What is the circumference and area of the trapezoid?
The isosceles trapezoid ABCD has bases of 18 cm and 12 cm. The angle at apex A is 60°. What is the circumference and area of the trapezoid? - Modulus and argument
 Find the mod z and argument z if z=i
Find the mod z and argument z if z=i - Horizontal 66434
 The lower station of the cable car in Smokovec is at an altitude of 1025m, and the upper station at Hrebienk is at an altitude of 1272m. Calculate the climb of the cable car if the horizontal distance between the slopes is 1921m.
The lower station of the cable car in Smokovec is at an altitude of 1025m, and the upper station at Hrebienk is at an altitude of 1272m. Calculate the climb of the cable car if the horizontal distance between the slopes is 1921m. - Rectangular
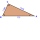 Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Hypotenuse and center
 Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°.
Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°. - Right triangle eq2
 Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70. - Toboggan run
 The length of the toboggan run is 60 m, and the height is 8 m. The boy pulls a sled weighing 15 kg. How hard does the boy pull the sled uphill?
The length of the toboggan run is 60 m, and the height is 8 m. The boy pulls a sled weighing 15 kg. How hard does the boy pull the sled uphill? - Tree
 Between points A and B is 50m. From A, we see a tree at an angle of 18°. From point B, we see the tree at a three times bigger angle. How tall is a tree?
Between points A and B is 50m. From A, we see a tree at an angle of 18°. From point B, we see the tree at a three times bigger angle. How tall is a tree? - Height difference
 What height difference is overcome if we pass a road 1 km long with a pitch of 21 per mille?
What height difference is overcome if we pass a road 1 km long with a pitch of 21 per mille? - Tree
 How tall is the tree observed at the visual angle 45°? If I stand 3 m from the tree, my eyes are two meters above the ground.
How tall is the tree observed at the visual angle 45°? If I stand 3 m from the tree, my eyes are two meters above the ground.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
