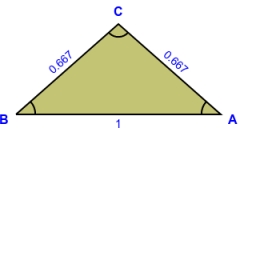
Isosceles triangle 10
In an isosceles triangle, the equal sides are 2/3 of the length of the base. Determine the measure of the base angles.
Final Answer:
Tips for related online calculators
Calculation of an isosceles triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles triangle
What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m? - Internal angles IST
Determine internal angles of isosceles trapezium ABCD /a, c are the bases/ and if: alpha:gamma = 1:3 - Isosceles triangle
An isosceles triangle with base c and arms a is given by: a = 50.3 cm c = 48.2 cm Determine the interior angles and heights of the base c. - An isosceles 2
An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame. - Two men 2
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men. - Determine 82143
Determine the size of the interior angles in an isosceles triangle if you know that the angle opposite the base is 15° greater than the angles at the base. - Angle at the apex
In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles?
