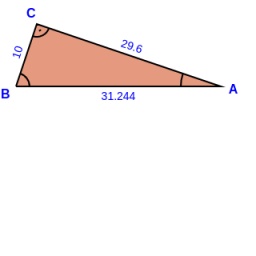
Right triangle
Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right triangle trigonometrics
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60° and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent) - Calculate 6687
Calculate the sizes of the remaining inner and outer angles. Alpha with comma α '= 140 ° and beta with comma β' = 100 °. - Angles of a triangle
In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle. - The triangles
The triangles ABC and A'B'C 'are similar with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35°, beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Magnitudes 64704
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Perimeter 27813
If given, calculate the sizes of the remaining sides of the right triangle ABC: alpha = 45 degrees and perimeter o = 125. Thank you - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC, if it is given by area S = 501.9; and two internal angles α = 15°28' and β = 45°. - One-quarter 13953
Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma. - Calculate 6678
You know the size of the two interior angles of the triangle alpha = 40 ° beta = 60 °. Calculate the size of the third interior angle. - Rectangular
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Calculate
Calculate the area of triangle ABC, if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm. - In triangle
In triangle ABC, the magnitude of the internal angle gamma is equal to one-third of the angle alpha. The size of the angle beta is 80 degrees larger than the size of the gamma angle. Calculate the magnitudes of the interior angles of the triangle ABC. - Circumscribed 6568
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - A trapezoid
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48° and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid. - The right triangle
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles. - Calculate 3209
Calculate the lengths of the sides of the triangle ABC, in which α = 113 °, β = 48 ° and the radius of the circle of the triangle described is r = 10 cm. - Triangle from median
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles, given: a = 8.4; β = 105° 35 '; and median ta = 12.5.
