Calculate 3209
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm.
Correct answer:
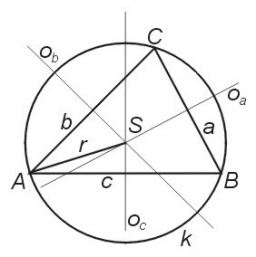
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right triangle
Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'. - Isosceles IV
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - A trapezoid
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid. - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
- Right triangle trigonometrics
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60°, and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent) - RT - inscribed circle
In a rectangular triangle has sides lengths> a = 30cm, b = 12.5cm. The right angle is at vertex C. Calculate the radius of the inscribed circle. - Hexagon 5
The distance of parallel sides of regular hexagonal is 61 cm. Calculate the length of the radius of the circle described in this hexagon. - Millimeters 4811
Construct a triangle ABC if you know the lengths of its sides c = 5 cm, a = 4 cm and angle ABC is 60°. Measure the length of side b in millimeters. Side length b is: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm - Sides ratio and angles
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
- Hypotenuses 83154
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Right-angled 64084
A right-angled triangle ABC with sides 5 cm and 12 cm is described by circle k. Calculate the length of circle k in centimeters. When calculating, use π = 3, 14 and round the result to tenths. - Isosceles - isosceles
It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB. - Calculate 58953
Calculate the area of a circular line if the radius r = 80 cm and the central angle is α = 110 °. - Quadrilateral 42151
Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o
- Calculate 3208
Calculate the size of the sides and angles of the triangle ABC if you know vc = 28, α = 51 ° 19 ', β = 67 ° 38'. - Cosine
Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Angles and sides of the triangle
Triangle ABC has a circumference of 26 cm. Lengths of the sides are as follows: a = 11.2 cm; b = 6.5 cm. Arrange the interior angles in order of their size. ...
