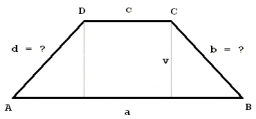
A trapezoid
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 42151
Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o - Calculate 3209
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm. - Rhomboid
The rhomboid sides' dimensions are a= 5cm, b = 6 cm, and the angle's size at vertex A is 60°. What is the length of the side AC? - Right triangle trigonometrics
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60°, and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent) - Four sides of trapezoid
Calculate the area of the ABCD trapezoid with sides a = 65 cm, b = 29 cm, c = 40 cm, d = 36 cm - Trapezoid 2520
Trapezoid with sides a = 10, b = 20, c = 25, d = 15. Calculate all internal angles. - Right triangle
Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'. - Four sides of trapezoid
In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles. - Calculate 3208
Calculate the size of the sides and angles of the triangle ABC, if you know vc = 28, α = 51 ° 19 ', β = 67 ° 38'. - Difference 2435
Calculate the sum and difference of the alpha and beta angles. Alpha = 60 ° 30 ', beta = 29 ° 35'. - Rectangular
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Four prisms
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t - Parallelogram 65334
In a parallelogram, the sum of the lengths of the sides a+b = 234. The angle subtended by the sides a and b is 60°. The diagonal size against the given angle of 60° is u=162. Calculate the sides of the parallelogram, its perimeter, and its area. - Area 4gon
Calculate the area of 4-gon, two, and the two sides are equal and parallel with lengths 11, 5, 11, and 5. Inner angles are 45°, 135°,45°, 135°. - Rectangular trapezoid
In a rectangular trapezoid ABCD with right angles at vertices A and D with sides a = 12cm, b = 13cm, c = 7cm. Find the angles beta and gamma and height v. - Circumference 7686
The circumference of the isosceles trapezoid is 34 cm. The difference in the length of the bases is 6 cm. The arm's length is one-third of the length of the longer base. Find the lengths of the trapezoidal sides. - An isosceles
An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area.
