Angle practice problems - page 26 of 64
Number of problems found: 1262
- Road
 Between cities, A and B is a route 9 km long of average 9‰ klesanie. Calculate the height difference between cities A and B.
Between cities, A and B is a route 9 km long of average 9‰ klesanie. Calculate the height difference between cities A and B. - Maggie
 Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree.
Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree. - View angle - river
 The 15 m high building is 30 m away from the river bank. The river's width can be seen from the roof of this building at an angle of 15°. How wide is the river?
The 15 m high building is 30 m away from the river bank. The river's width can be seen from the roof of this building at an angle of 15°. How wide is the river? - Ratio iso triangle
 The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures.
The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures. - Cablecar
 Funicular on Petrin (Prague) was 408 meters long and overcame the difference of 106 meters in altitude. Calculate the angle of the climb.
Funicular on Petrin (Prague) was 408 meters long and overcame the difference of 106 meters in altitude. Calculate the angle of the climb. - Cable car 2
 The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track?
The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track? - Elevation 80866
 Find the height of the tower when the geodetic measured two angles of elevation α=34° 30'' and β=41°. The distance between places AB is 14 meters.
Find the height of the tower when the geodetic measured two angles of elevation α=34° 30'' and β=41°. The distance between places AB is 14 meters. - Difference 81888
 The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture
The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture - The airplane
 The airplane sights a runway at an angle of depression of 23°. It is flying at an altitude of 3 kilometers above the ground. What is the horizontal distance of the airplane from the airport?
The airplane sights a runway at an angle of depression of 23°. It is flying at an altitude of 3 kilometers above the ground. What is the horizontal distance of the airplane from the airport? - Calculate 2575
 Calculate the area and height of the rhombic cover plate to which the following applies: d (BC) = 60 cm, angle BAD = 45 °, angle ADB = 90 °.
Calculate the area and height of the rhombic cover plate to which the following applies: d (BC) = 60 cm, angle BAD = 45 °, angle ADB = 90 °. - Ratio of triangles areas
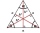 In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - How far
 From the top of a lighthouse 145 ft above sea level, the angle of depression of a boat is 29°. How far is the boat from the lighthouse?
From the top of a lighthouse 145 ft above sea level, the angle of depression of a boat is 29°. How far is the boat from the lighthouse? - Church tower
 Archdeacon church in Usti nad Labem has diverted the tower by 186 cm. The tower is 65 m high. Calculate the angle by which the tower is tilted. Results are written in degree minutes.
Archdeacon church in Usti nad Labem has diverted the tower by 186 cm. The tower is 65 m high. Calculate the angle by which the tower is tilted. Results are written in degree minutes. - Complex square roots
 Determine the sum of the three square roots of 343.
Determine the sum of the three square roots of 343. - Interior 39791
 For the interior angles of a triangle, the angle β is twice as large, and the angle γ is three times larger than the angle α. Is this triangle right?
For the interior angles of a triangle, the angle β is twice as large, and the angle γ is three times larger than the angle α. Is this triangle right? - Determine 39503
 In a right triangle, one acute angle is 20° smaller than the other. Determine the size of the interior angles in the triangle.
In a right triangle, one acute angle is 20° smaller than the other. Determine the size of the interior angles in the triangle. - Angles in a triangle
 In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle?
In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle? - The right triangle
 In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles.
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles. - Right angled triangle 3
 Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides.
Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides. - The interior
 The interior angle of a regular polygon is x. If x is 9° less than the average of 153° and 145°, find the number of sides of the polygon.
The interior angle of a regular polygon is x. If x is 9° less than the average of 153° and 145°, find the number of sides of the polygon.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
