Arctangent - practice problems - page 4 of 5
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 91
- Resultant force
Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25° - Cone
The rotating cone volume is 9.42 cm3, with a height of 10 cm. What angle is between the side of the cone and its base? - Clouds
From two points, A and B, on the horizontal plane, a forehead cloud was observed above the two points under elevation angles 73°20' and 64°40'. Points A and B are separated by 2830 m. How high is the cloud? - Directional 2595
Calculate the interior angles of triangle ABC using vectors. Coordinates A [2; 4] B [4; 6] C [0; -4]. Calculate directional vectors of sides, parametric and general equations of sides, parametric and general equations of lines, calculate area, calculate h - Road drop
A 12 percent drop is marked on a straight stretch of road. What angle aligns the direction of the road with the horizontal plane? - Church tower
Archdeacon church in Usti nad Labem has diverted the tower by 186 cm. The tower is 65 m high. Calculate the angle by which the tower is tilted. Results are written in degree minutes. - Height difference
What height difference is overcome if we pass a road 1 km long with a pitch of 21 per mille?
- Railway
The railway line had a 5.8 km segment climb nine permille. How many meters does the track ascent? - Two forces
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer. - Bevel
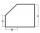I have a bevel in the ratio 1:6. What is the angle, and how do I calculate it? - Sphere in cone
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions. - Cuboid
Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine the angle between the body diagonal and the base plane (round to degrees). - Angle A straight line p given by the equation y = (-8)/(6) x +78. Calculate the size of the angle in degrees between line p and y-axis.
- Slope of the pool
Calculate the slope (ratio rise:run) of the bottom of the swimming pool long 40 m. The water depth at the beginning of the pool is 1.09 m (for children), and the depth at the end is 1.88 m (for swimmers). Calculated slope write it as a percentage and also - Map - climb
On the map of the High Tatras, on a scale of 1:11000, are cable car stations in the Tatranska Lomnica and the Skalnate Pleso with a distance of 354.6 mm. The altitude of these stations is 949 m and 1760 m. What is the average angle of climb on this cable
- Pyramid
The pyramid has a base a = 2cm and height in v = 7 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side. - Goniometric form
Determine the goniometric form of a complex number z = √ 110 +4 i. - Road
A ratio of 1:15 gives the average climb of the road. By what angle does the road moderate climb? - Stairway
What angle rising stairway if the step height is 20 cm and the width 26 cm? - River
From the observatory 18 m high and 31 m from the riverbank, river width appears in the visual angle φ = 20°. Calculate the width of the river.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
