Two forces
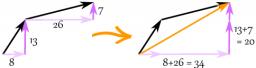
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer.
Correct answer:
Showing 1 comment:
Dr Math
Angle 100-10 = 90° is right , therefore may be some optimization of calculation made. In general it§s calculated OK.
See also vector adding calculator:
https://www.hackmath.net/en/calculator/sum-of-the-two-vectors?a=25&a1=100-10&b=30&submit=Solve
See also vector adding calculator:
https://www.hackmath.net/en/calculator/sum-of-the-two-vectors?a=25&a1=100-10&b=30&submit=Solve
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- vector
- arithmetic
- square root
- rounding
- addition
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- numbers
- fractions
- goniometry and trigonometry
- sine
- cosine
- tangent
- arctangent
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Mass point
Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°. - Two forces 3
Two forces with magnitudes 8 Newtons and 15 Newtons act at a point. Find the angle between the forces if the resultant force is 17 Newtons. - Forces
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant? - Perpendicular 81758
Distribute the force of magnitude F = 100 N into two perpendicular components with magnitudes F1 and F2 so that the angle between forces F1 and F is 43°52'.
- A man 7
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles toward N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - Resultant force
Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25° - Similarity coefficient
The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'.
