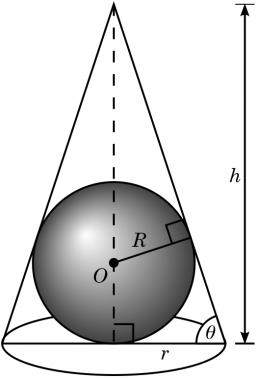
Sphere in cone
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
geometryalgebrasolid geometryplanimetricsbasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Sphere and cone
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Cone
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder. - Cross-sections of a cone
Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Sphere submerged in the cone
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Vertex angle - cone
The rotating cone has a height of 72 cm and an angle at the top of 72°. Determine the volume of a sphere with the same radius as the cone. - Two Sections
A sphere with a radius of 5 cm was divided into two spherical sections. The height of the smaller section is 1cm. Determine the volume of the smaller section to the nearest hundredth of a cm³. - Calculate 45991
Calculate the radius of a sphere with the same volume as a cone with a radius of 5cm and a height of 7cm.
