Guľa v kuželi

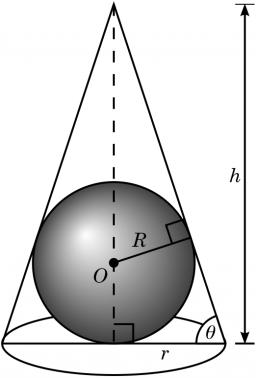
Guľi o polomere 3 cm opíšte kužeľ minimálneho objemu. Určte jeho rozmery.

Správna odpoveď:

Našiel si chybu či nepresnosť? Kľudne nám ju napíš.

Zobrazujem 1 komentár:

Dr. Math

Iné riešenie - bez uhlov - na vyriešenie tejto úlohy potrebujeme nájsť rozmery kužeľa minimálneho objemu, ktorý je opísaný guli s polomerom r = 3 cm.

Postup riešenia:

1. Označenie premenných:
- Polomer gule: r = 3 cm.
- Polomer základne kužeľa: R .
- Výška kužeľa: H .
- Vznikajúci pravouhlý trojuholník: podobnosť trojuholníkov.

2. Vzťah medzi R , H a r :
Z podobnosti trojuholníkov v rezovej rovine kužeľa a gule dostaneme:

H - r √R² + H² = rR

Po úprave:

R(H - r) = r √R² + H²

Vynásobením oboch strán R a následnou úpravou:

R²(H - r)² = r²(R² + H²)

Rozšírením a zjednodušením:

H² R² - 2 H r R² + r² R² = r² R² + r² H²

H² R² - 2 H r R² = r² H²

H R² - 2 r R² = r² H

R² (H - 2r) = r² H

R² = r² HH - 2r

3. Objem kužeľa:
Objem kužeľa je daný vzťahom:

V = 13 π R² H

Dosadením R² z predchádzajúceho vzťahu:

V = 13 π ( r² HH - 2r ) H = π r² H²3(H - 2r)

4. Minimalizácia objemu:
Hľadáme minimum funkcie V(H) . Zderivujeme V podľa H a nastavíme deriváciu na nulu:

dVdH = π r² [2H(H - 2r) - H²]3(H - 2r)² = 0

Čitateľ sa rovná nule:

2H(H - 2r) - H² = 0

2H² - 4rH - H² = 0

H² - 4rH = 0

H(H - 4r) = 0

Pre H > 2r (aby bol menovateľ kladný) dostaneme:

H = 4r

Pre r = 3 cm:

H = 12 cm

5. Výpočet polomeru R :
Dosadením H = 4r do vzťahu pre R² :

R² = r² · 4r4r - 2r = 4r³2r = 2r²

R = r √2 = 3 √2 cm

Výsledné rozmery kužeľa:

- Výška kužeľa:

12 cm

- Polomer základne kužeľa:

3 √2 cm

6 dní Like

Tipy na súvisiace online kalkulačky

Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.