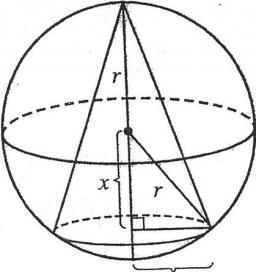
Sphere and cone

Within the sphere of radius G = 33 cm inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone?

Correct result:

r = 31.11 cm
h = 44 cm
V = 44602.24 cm³

Solution:

G = 33 c m V = \frac{1}{3} π r^{2} h h = G + x = 33 + x G^{2} = x^{2} + r^{2} r^{2} = G^{2} - x^{2} V = \frac{1}{3} π (G^{2} - x^{2}) (G + x) V = \frac{1}{3} π (G^{3} + G^{2} x - G x^{2} - x^{3}) V^{'} = \frac{1}{3} π (G^{2} - 2 G x - 3 x^{2}) V^{'} = 0 G^{2} - 2 G x - 3 x^{2} = 0 - 3 x^{2} - 66 x + 1089 = 0 3 x^{2} + 66 x - 1089 = 0 a = 3; b = 66; c = - 1089 D = b^{2} - 4 a c = 6 6^{2} - 4 \cdot 3 \cdot (- 1089) = 17424 D > 0 x_{1, 2} = \frac{- b \pm \sqrt{D}}{2 a} = \frac{- 66 \pm \sqrt{17424}}{6} x_{1, 2} = \frac{- 66 \pm 132}{6} x_{1, 2} = - 11 \pm 22 x_{1} = 11 x_{2} = - 33 Factored form of the equation: 3 (x - 11) (x + 33) = 0 h = G + x_{1} = 33 + 11 = 44 c m r = \sqrt{G^{2} - x_{1}^{2}} = 31.11 cm

h = 33 + 11 = 44 cm

V = \frac{1}{3} π r^{2} h = 44602.24 {cm}^{3}

Our quadratic equation calculator calculates it.

Try another example

We would be pleased if you find an error in the word problem, spelling mistakes, or inaccuracies and send it to us. Thank you!

Showing 1 comment:

Dr Math

that's very mind blowing

2 years ago Like

Tips to related online calculators

Looking for help with calculating roots of a quadratic equation?
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

We encourage you to watch this tutorial video on this math problem: video1 video2 video3

Next similar math problems:

Sphere in cone
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions.
Cone
Into rotating cone with dimensions r = 8 cm and h = 8 cm incribe cylinder with maximum volume so that the cylinder axis is perpendicular to the axis of the cone. Determine the dimensions of the cylinder.
Cube in sphere
The sphere is inscribed cube with edge 8 cm. Find the radius of the sphere.
Cuboid
Cuboid with edge a=6 cm and space diagonal u=31 cm has volume V=900 cm³. Calculate the length of the other edges.
Secret treasure
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base 4 m and a height of 3 m. Determine the radius r (and height h) of the container so that they can hide the largest possible treasure.
Paper box
Hard rectangular paper has dimensions of 60 cm and 28 cm. The corners are cut off equal squares and the residue was bent to form an open box. How long must be side of the squares to be the largest volume of the box?
Body diagonal
Calculate the length of the body diagonal of a block with dimensions: a = 20 cm, b = 30 cm, c = 15 cm.
Tangent spheres
A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it? Additional info: Two spheres are placed in a corner of a room. The spheres are each tangent to the walls and floor and
Two balls
Two balls, one 8cm in radius and the other 6cm in radius, are placed in a cylindrical plastic container 10cm in radius. Find the volume of water necessary to cover them.
Truncated cone 5
The height of a cone 7 cm and the length of side is 10 cm and the lower radius is 3cm. What could the possible answer for the upper radius of truncated cone?
Ratio of edges
The dimensions of the cuboid are in a ratio 3: 1: 2. The body diagonal has a length of 28 cm. Find the volume of a cuboid.
Cut and cone
Calculate the volume of the rotation cone which lateral surface is circle arc with radius 15 cm and central angle 63 degrees.
Cube and sphere
Cube with the surface area 150 cm² is described sphere. What is sphere surface?
The diagram 2
The diagram shows a cone with slant height 10.5cm. If the curved surface area of the cone is 115.5 cm². Calculate correct to 3 significant figures: *Base Radius *Height *Volume of the cone
Solid cuboid
A solid cuboid has a volume of 40 cm³. The cuboid has a total surface area of 100 cm squared. One edge of the cuboid has a length of 2 cm. Find the length of a diagonal of the cuboid. Give your answer correct to 3 sig. Fig.
Cone
Calculate the volume of the rotating cone with a base radius 26.3 cm and a side 38.4 cm long.
Maximum of volume
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?