Area of Right triangle Problems - page 16 of 30
Number of problems found: 595
- Isosceles trapezoid
 The old father decided to change the top plate of an isosceles-like trapezoid, which has basic dimensions of 120 cm and 60 cm, and a shoulder that is 50 centimeters long. How much does it pay for a new plate and a square meter worth 17 euros?
The old father decided to change the top plate of an isosceles-like trapezoid, which has basic dimensions of 120 cm and 60 cm, and a shoulder that is 50 centimeters long. How much does it pay for a new plate and a square meter worth 17 euros? - Advertising Board Rent Cost
 Renting a 1m² advertising board costs €780 per month. A rectangular advertising board has a length of 3 m and its diagonal makes an angle of 34 degrees with the longer side. Calculate how much € an entrepreneur will pay for 4 months of renting a blackboar
Renting a 1m² advertising board costs €780 per month. A rectangular advertising board has a length of 3 m and its diagonal makes an angle of 34 degrees with the longer side. Calculate how much € an entrepreneur will pay for 4 months of renting a blackboar - Kite rhombus calculation
 The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend.
The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend. - Metal washers
 Metal washers with a diameter of 80 mm are cut from a strip of steel sheet with a width of 10 cm and a length of 2 m. When two adjacent circles meet, calculate the material waste percentage if no material is lost.
Metal washers with a diameter of 80 mm are cut from a strip of steel sheet with a width of 10 cm and a length of 2 m. When two adjacent circles meet, calculate the material waste percentage if no material is lost. - Perpendicular sides
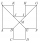 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ - Rectangular roof
 Our house's roof is rectangular. When it rains, the water drains through the gutter. How much water flowed from our roof during a storm when we know that 12 liters of water fell on every 1 m² of surface? The roof width is 6m, the length is 9m, and the slo
Our house's roof is rectangular. When it rains, the water drains through the gutter. How much water flowed from our roof during a storm when we know that 12 liters of water fell on every 1 m² of surface? The roof width is 6m, the length is 9m, and the slo - Widescreen monitor
 A wave of widescreen monitors and televisions hit computer businesses. Calculate the area of the LCD monitor with a diagonal size 27 inches at a ratio of 4:3 and then a 16:9 aspect ratio. Is buying widescreen monitors with the same diagonal more advanta
A wave of widescreen monitors and televisions hit computer businesses. Calculate the area of the LCD monitor with a diagonal size 27 inches at a ratio of 4:3 and then a 16:9 aspect ratio. Is buying widescreen monitors with the same diagonal more advanta - Flowerbed
 The family has tulips on a square flower bed of 6 meters. Later, they added a square terrace with a side of 7 meters to their house. One vertex of the terrace lay exactly in the middle of a tulip bed, and one side of the terrace was divided by the side of
The family has tulips on a square flower bed of 6 meters. Later, they added a square terrace with a side of 7 meters to their house. One vertex of the terrace lay exactly in the middle of a tulip bed, and one side of the terrace was divided by the side of - Triangle - many properties
 In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - Trapezoid field
 The field between the two parallel roads is shaped like a trapezoid with 180m and 100m long bases. The distance between the roads is 80m. When the yield of this type of cereal is 8.5 tons from 1 hectare, how many tons of barley were harvested in the field
The field between the two parallel roads is shaped like a trapezoid with 180m and 100m long bases. The distance between the roads is 80m. When the yield of this type of cereal is 8.5 tons from 1 hectare, how many tons of barley were harvested in the field - Isosceles triangle 9
 There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle.
There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle. - Nonagon
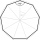 Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm.
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Goat and circles
 What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which - Central park in city
 The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou
The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou - Isosceles trapezoid 3
 In the isosceles trapezoid ABCD, calculate the unknown side length "a" and its area. Side b = d = 50 cm, c = 20 cm, height = 48 cm.
In the isosceles trapezoid ABCD, calculate the unknown side length "a" and its area. Side b = d = 50 cm, c = 20 cm, height = 48 cm. - Chocolate roll
 The cube of a 5 cm chocolate roll weighs 30 g. How many calories will the identical chocolate roller of a prism shape with a length of 0.5 m whose cross-section is an isosceles trapezoid with bases 25 and 13 cm and legs 10 cm contain? You know that 100 g
The cube of a 5 cm chocolate roll weighs 30 g. How many calories will the identical chocolate roller of a prism shape with a length of 0.5 m whose cross-section is an isosceles trapezoid with bases 25 and 13 cm and legs 10 cm contain? You know that 100 g - Gardens
 The square garden is 3/4 of the area of the triangular garden, which has sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden?
The square garden is 3/4 of the area of the triangular garden, which has sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden? - Triangle height intersection
 Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides.
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides. - Diagonals at right angle
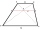 In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
