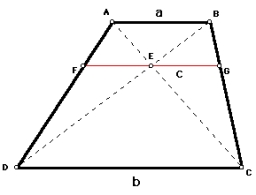
Diagonals at right angle
In the trapezoid ABCD, this is given:
AB=12cm
CD=4cm
And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
AB=12cm
CD=4cm
And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
Correct answer:
Showing 1 comment:
Math student
I don't think the solution is correct. The height is the radius if and only if the trapezoid is symmetrical. But it doesn't have to be. In fact, take a line segment of length 12 and start a 20 degree angle from one side and 70 from the other (for the diagonals). Intersect them and keep going until there is 4 long parallel line. Then increase the 20 degree angle - the height will increase and the area too.
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- geometry
- Thales' theorem
- similarity of triangles
- planimetrics
- right triangle
- area of a shape
- triangle
- trapezoid
- diagonal
- basic functions
- functions
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles 37621
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Circumference 7052
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Trapezium diagonals
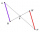It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Trapezoid: 18703
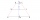In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Trapezoid 70454
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal. - Isosceles 2588
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |, on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Trapezoid 20873 In the trapezoid ABCD (AB II CD) is α = 57 °, γ = 4β. Calculate the size of all interior angles.
- Diamond area from diagonals
In the diamond, ABCD is AB = 4 dm, and the length of the diagonal is 6.4 dm long. What is the area of the diamond? - Swimming pool
A swimming pool 30 meters long is filled with water to a depth of 1 meter at the shallow end, and 5 meters at the deep end and abcd the vertical area of the pool has the shape of a trapezium with the area given by S(abcd)= 1/2 (ab + cd) x ad. What is the - Rectangular trapezoid
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate trapezium area in cm square and calculate how many differs perimeters of the - Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - Four-digit number
For a four-digit number abcd, ab: bc = 1: 3 and bc: cd = 2: 1 (ab, bc and cd are two-digit numbers from digits a, b, c, d). Find this number(s). - Trapezoid
The rectangular trapezoid ABCD with right angle at the vertex A has sides a, b, c, d. Calculate the circumference and the area of the trapezoid if given: a = 25cm, c = 10cm, d = 8cm - Trapezoid - diagonal
A trapezoid has a length of diagonal AC crossed with diagonal BD in the ratio 2:1. The triangle created by points A, cross point of diagonals S and point D has area 164 cm². What is the area of the trapezoid? - Trapezoid ABCD
ABDC is a trapezoid in which AB and CD are parallel sides measuring 6 and 9, respectively. Angles ABC and BCD are both right angles. Find the length of segment BD.
