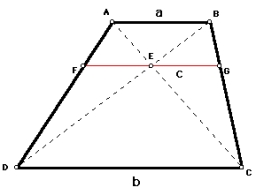
V lichoběžníku

V lichoběžníku ABCD jsou dány základny:
AB = 12cm
CD = 4 cm
A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD?

Správná odpověď:

S =  64 cm2

Postup správného řešení:

a=12 cm c=4 cm  a:c = h1​:h2​  h = h1​+h2​  h1​=a/2=12/2=6 cm h2​=c/2=4/2=2 cm  h=h1​+h2​=6+2=8 cm  S=2a+c​⋅ h=212+4​⋅ 8=64 cm2

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.



Zobrazuji 11 komentářů:
Michal
Není mi jasné, proč by muselo platit, že h1 = a/2  nebo h2 = c/2

6 let  1 Like
Dr Math
no h1 = a/2 je pripad kdyz se uhlopricky i puli....

Michal
Jenže tady se úhlopříčky nepůlí a ani nejsou stejně dlouhé.

Michal
Narýsoval jsem si v interaktivní geometrii lichoběžník ABCD s kolmými úhlopříčkami a základnami 12 a 4 cm. Existuje jich nekonečně mnoho, ale pouze v rovnoramenném by platilo vaše řešení.  Zadání není úplné nebo úloha nejde jednoznačně vyřešit.

Dr Math
Ale uloha nema otazku ze ci existuje nekonecne vela kolmych uhlopricek. Uloha sa pyta na obsah a ten muze byt i pre nekonecne vela lichobezniku rovnaky... protoze soucet vysek h1+h2 bude stale konstanta

Žák
No to právě nebude, protože průsečík kolmých úhlopříček musí ležet na kružnici sestrojené nad základnou jako jejím průměrem, viz Thaletova kružnice. A u ostatních lichoběžníků než rovnoramenných bude vždy nižší než 8 cm

Mathgebra
Nick Michal má pravdu. Vzorec (a+c)/2 . h platí jen tehdy, pokud je h kolmé na základny. Ale dle výpočtu, že h1 = a/2 to ukazuje, že h1 a h2 jsou pouze TĚŽNICE (doprostřed) nikoliv výšky (kolmé). Leda by byly obě kolmé úhlopříčky ze zadání stejně dlouhé, což ale řečeno nebylo.

Žák
Lze vypočítat úhlopříčku v lichoběžníku?

Lucie
Dobrý den, mám stejnou otázku jako žák, který ji napsal přede mnou. Mám za úkol do matematiky napsat délku úhlopříčky. Lze to vypočítat? Popřípadě jak? (Ještě jsme nebrali cos, sin, ...)
Předem moc děkuji za odpověď.

Zs Ucitel
no zkuste pyt. vetu. Ak se neco protina v pravem uhlu... Pak Pytagorova veta pomuze...

sin cos vedy ked znam uhly... (najma jine ako 90 st.)

Lenka
Ak použijeme priložený obrázok, a na základňu CD urobíme kolmicu k a úsečku AB predĺžime za bod B ich priesečník nech je B´ a vzdialenosť AB´ nech je "x". Uhol BDC nech je beta.
Platí tg(beta) =(x/h)=(h/(16-x)) pre h platí h= (16x-x2)0,5 a pre plochu lichobežníka platí:
S=8*(16x-x2)0,5; ak zároveň x patrí do intervalu 4cm až 12cm.
S=64cm2 je v tomto íntervale maximálna hodnota.





Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

geometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu

Související a podobné příklady: