Area of Square Problems - page 66 of 79
Number of problems found: 1580
- Triangular Prism Volume
 A three-sided prism has a base in the shape of a right-angled triangle with a length of 5 cm. The giant wall of the prism shell has a volume of 104 cm². The prism is 8 cm high. Calculate the volume and surface area of the prism.
A three-sided prism has a base in the shape of a right-angled triangle with a length of 5 cm. The giant wall of the prism shell has a volume of 104 cm². The prism is 8 cm high. Calculate the volume and surface area of the prism. - Square prism
 Calculate the volume of a square prism of high 2 dm wherein the base is: Rectangle with sides of 17 cm and 1.3 dm
Calculate the volume of a square prism of high 2 dm wherein the base is: Rectangle with sides of 17 cm and 1.3 dm - Cone
 The rotating cone volume is 9.42 cm3, with a height of 10 cm. What angle is between the side of the cone and its base?
The rotating cone volume is 9.42 cm3, with a height of 10 cm. What angle is between the side of the cone and its base? - Centimeters - block
 The surface of the block is 4596 square centimeters. Its sides are in a ratio of 2:5:4. Calculate the volume of this block.
The surface of the block is 4596 square centimeters. Its sides are in a ratio of 2:5:4. Calculate the volume of this block. - Truncated pyramid
 How many cubic meters is the volume of a regular four-sided truncated pyramid with edges of one meter and 60 cm and a high of 250 mm?
How many cubic meters is the volume of a regular four-sided truncated pyramid with edges of one meter and 60 cm and a high of 250 mm? - Axial section
 The axial section of the cylinder has a diagonal 50 cm. The shell size and base surface are in the ratio 2:5. Calculate the volume and surface area of this cylinder.
The axial section of the cylinder has a diagonal 50 cm. The shell size and base surface are in the ratio 2:5. Calculate the volume and surface area of this cylinder. - Cone and the ratio
 The rotational cone has a height of 59 cm, and the ratio of the base surface to the lateral surface is 10: 12. Calculate the surface of the base and the lateral surface.
The rotational cone has a height of 59 cm, and the ratio of the base surface to the lateral surface is 10: 12. Calculate the surface of the base and the lateral surface. - The pot
 The pot is in 1/3 filled with water. The bottom of the pot has an area of 329 cm². How many centimeters rise in water level in the pot after adding 1.2 liters of water?
The pot is in 1/3 filled with water. The bottom of the pot has an area of 329 cm². How many centimeters rise in water level in the pot after adding 1.2 liters of water? - Classroom painting cost
 The classroom is 11 m long. The width is 6.5 m, and the height is 4 m. We will pay CZK 7.50 for 1 m of square painting. How much will it cost to paint a classroom? They rounded to the crowns.
The classroom is 11 m long. The width is 6.5 m, and the height is 4 m. We will pay CZK 7.50 for 1 m of square painting. How much will it cost to paint a classroom? They rounded to the crowns. - Roof sheet calculation
 Above the pavilion, with a square floor plan with side a = 12 m, is a pyramid-shaped roof with a height of 4.5 m. How many m² of sheet metal is needed to cover this roof?
Above the pavilion, with a square floor plan with side a = 12 m, is a pyramid-shaped roof with a height of 4.5 m. How many m² of sheet metal is needed to cover this roof? - Paint cans
 The room has 4m, 5m, and 2.4m dimensions. Suppose one can is enough to paint 10 m². How many cans of paint are needed to paint the walls and ceiling of this room?
The room has 4m, 5m, and 2.4m dimensions. Suppose one can is enough to paint 10 m². How many cans of paint are needed to paint the walls and ceiling of this room? - 4B - truncated pyramid
 Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm.
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm. - Hip-roof
 The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar
The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar - Spherical segment
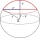 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm. - Dimensions - cardboard
 The statements are sold in cardboard boxes – for example, the microwave oven box has dimensions of 52 cm, 32 cm, and 40 cm, and 0.4 m² of cardboard is added to the folds. How many square meters of cardboard are needed for 1,000 boxes?
The statements are sold in cardboard boxes – for example, the microwave oven box has dimensions of 52 cm, 32 cm, and 40 cm, and 0.4 m² of cardboard is added to the folds. How many square meters of cardboard are needed for 1,000 boxes? - Hexagonal wax
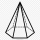 The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax.
The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax. - Water level
 What is the area of the pool's water level after filling 25 m³ of water level by 10 cm? a) 25 m² b) 250 m² c) 2500 dm² d) 25,000 cm2
What is the area of the pool's water level after filling 25 m³ of water level by 10 cm? a) 25 m² b) 250 m² c) 2500 dm² d) 25,000 cm2 - Volleyball - air in ball
 The radius of a volleyball is 10 cm. Calculate how many liters of air fit into an ideal inflated ball. Calculate how many square meters of leather material you need to make it.
The radius of a volleyball is 10 cm. Calculate how many liters of air fit into an ideal inflated ball. Calculate how many square meters of leather material you need to make it. - Cutting the prism
 A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism?
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Pyramid volume calculation
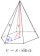 Calculate the volume of a regular quadrilateral pyramid, which has the size of the base edge a = 8 cm and the length of the side edge h = 9 cm.
Calculate the volume of a regular quadrilateral pyramid, which has the size of the base edge a = 8 cm and the length of the side edge h = 9 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
