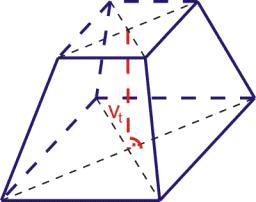
Truncated pyramid
How many cubic meters is the volume of a regular four-sided truncated pyramid with edges of one meter and 60 cm and a high of 250 mm?
Correct answer:
Tips for related online calculators
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
Do you know the volume and unit volume, and want to convert volume units?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Truncated 43851
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6m. Calculate how much m³ of soil was removed when we dug this pit. - Digging a pit
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - Quadrilateral 5814
Calculate the surface area and volume of a regular quadrilateral truncated pyramid if the base edges are 87 cm and 64 cm and the wall height is 49 cm. - Quadrilateral 81033
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases.
- Truncated pyramid
Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees. - Runcated pyramid teapot
The 35 cm high teapot has the shape of a truncated pyramid with the length of the edge of the lower square base a=50 cm and the edges of the rectangular base b: 20 cm and c: 30 cm. How many liters of water will fit in the teapot? - Base diagonal
In a regular four-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the pyramid's surface area and volume.
