Area of Triangle Problems - page 27 of 42
Number of problems found: 837
- Centimeters 80859
Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm². - Diagonals 14073
There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you - Isosceles 7566
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Square
Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD. - Coordinates
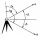Determine the coordinates of the vertices and the area of the parallelogram, the two sides of which lie on the lines 8x + 3y + 1 = 0, 2x + y-1 = 0, and the diagonal on the line 3x + 2y + 3 = 0 - Hypotenuse - RT
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Circular segment
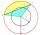Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Right-angled 78394
A right-angled triangle was inscribed in a circle with a diameter of 20 cm, whose hypotenuse is the circle's diameter and has the largest possible area. Calculate the area of this triangle. - Circumscribed triangle
Calculate the radius of the circle of the circumscribed triangle, which has side dimensions of 8, 10, and 14 cm. - The triangle 5
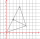The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - XY triangle
Determine the area of a triangle given by line 2x-4y+47=0 and coordinate axes x and y. - Triangle 69144
The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle? - Right-angled 40961
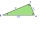A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate the percentage of the area of triangle ABC that is the area of triangle A'B'C'. - construction triangle problem
Construct the vertices C of all triangles ABC, if given side AB, height vb on side b, and length of line tc on side c. Build all the solutions. Mark the vertices C1, C2,. .. - Trapezoid 4908
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - A circle 2
A circle is centered at the point (-7, -1) and passes through the point (8, 7). The radius of the circle is r units. The point (-15, y) lies in this circle. What are r and y (or y1, y2)? - Inscribed circle
Write the equation of an incircle of the triangle KLM if K [2,1], L [6,4], M [6,1]. - Similarity of squares
The ratio of the similarity of the squares ABCD and KLMN is 2.5. Square KLMN area is greater than an area of a square ABCD with side a: ... - Trapezoid IV
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
