Trapezoid IV
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD?
Final Answer:
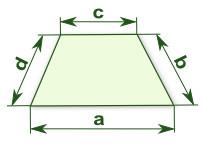
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsgoniometry and trigonometryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm and CD = 4cm. Calculate the length of the AC diagonal. - Trapezoid: 18703
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Trapezoidal prism
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Circumference 7052
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Trapezoid - construction
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Trapezoid 4908
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - Rectangular trapezoid
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
