Area - math word problems - page 127 of 158
Number of problems found: 3149
- Cube walls
The wall of the cube has an area of 8 cm square. How many square cm is the surface of the cube? - Wall height
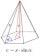Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm. - Four sides of trapezoid
The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area. - Dimensions 3408
The room has 4m, 5m, and 2.4m dimensions. Suppose one can is enough to paint 10 m². How many cans of paint are needed to paint the walls and ceiling of this room? - Dimensions 3406
We poured 3 liters of water into an empty aquarium, with a bottom dimension of 30x30cm and a height of 25cm. What is the level? - Axial cut
The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume. - Pyramid 4sides
Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm. - Support colum
Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m. - Traffic cones
Forty identical traffic cones with a base diameter d = 3 dm and height v = 6 dm will be painted orange outside (without the base). If we need 50 cm³ of paint to cover 1 m² and 1 liter of paint costs 80 SKK, how many SKK crowns will we pay? - Rotating cone
Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm. - Cube diagonals
If you know the length of the body diagonal u = 216 cm, determine the cube's volume and surface area. - Two-thirds 3388
The kneaded cake dough has a volume of 1.8 l. When baking, it increases its volume by about two-thirds. Can a baked wheel fit on a baking sheet measuring 36x30x8cm? How tall will the cake be after baking? - Pyramid
The pyramid has a base rectangle with a = 6cm and b = 8cm. The side edges are the same, and their length is 12.5 cm. Calculate the surface of the pyramid. - Quarter-liter 3380
A container has the shape of a regular hexagonal prism with a base and a capacity of 0.5 dm2, which means three quarter-liter cups of water fill the brim. What is the height of a container? - Cuboid and ratio
A cuboid has dimensions in a ratio of 1:2:6, and the surface area of the cuboid is 1000 dm². Calculate the volume of the cuboid. - Cone
The rotating cone volume is 9.42 cm3, with a height of 10 cm. What angle is between the side of the cone and its base? - The road
The road roller has a diameter of 1.2 m and a width of 180 cm. How many m² of the road does it level when it turns 35 times? - Folded square
ABCD is a square. The square is folded on the midpoint of AB, and A is folded onto the fold, creating a shaded region. The perimeter of the shaded figure is 75. Find the area of square ABCD - Hexagonal pyramid
A regular hexagonal pyramid has dimensions: the length edge of the base a = 1.8 dm, and the height of the pyramid = 2.4 dm. Calculate the surface area and volume of a pyramid. - Circumference 3370 Calculate the surface and volume of the rotating cone, whose base circumference is 125.6 cm and the side is 25 cm long.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
