Geometry - math word problems - page 60 of 162
Number of problems found: 3238
- Length of the edge
 Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number.
Find the length of the edge of a cube with a cm² surface and a volume in cm³ expressed by the same number. - Truncated cone and sphere
 A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter?
A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter? - Trapezoidal 24731
 Calculate how many candies fit in a box shaped like a 4-sided prism with a trapezoidal base with base dimensions of 20 cm and 3.2 cm. The distance between the bases is 50 mm. The container is 32 cm high, and 1 candy occupies 2.5 cm³ of volume.
Calculate how many candies fit in a box shaped like a 4-sided prism with a trapezoidal base with base dimensions of 20 cm and 3.2 cm. The distance between the bases is 50 mm. The container is 32 cm high, and 1 candy occupies 2.5 cm³ of volume. - Tank 28
 The tank is shaped like a cuboid. The bottom is rectangular, one side of the rectangle is 40cm long, and the diagonal of this rectangle is 50cm. The height of the tank is 1.5m. We start filling the tank with water at a rate of 1 liter per second. No water
The tank is shaped like a cuboid. The bottom is rectangular, one side of the rectangle is 40cm long, and the diagonal of this rectangle is 50cm. The height of the tank is 1.5m. We start filling the tank with water at a rate of 1 liter per second. No water - Iron rod
 What is the mass of a cylindrical iron rod with a length a = 9 m and a diameter d = 6 cm? The density of iron is 7,800 kg/m³. Express the result in kilograms, and round to the nearest whole number.
What is the mass of a cylindrical iron rod with a length a = 9 m and a diameter d = 6 cm? The density of iron is 7,800 kg/m³. Express the result in kilograms, and round to the nearest whole number. - Wooden box
 The block-shaped box was placed on the ground, leaving a rectangular print with 3 m and 2 m. When flipped over to another wall, a print with dimensions of 0.5 m and 3 m remained in the sand. What is the volume of the wooden box?
The block-shaped box was placed on the ground, leaving a rectangular print with 3 m and 2 m. When flipped over to another wall, a print with dimensions of 0.5 m and 3 m remained in the sand. What is the volume of the wooden box? - Pyramid a+h
 Calculate the pyramid's volume and surface area with the edge and height a = 26 cm. h = 3 dm.
Calculate the pyramid's volume and surface area with the edge and height a = 26 cm. h = 3 dm. - Cu wire
 Copper wire has a length l = 820 m and diameter d = 10 mm. Calculate the weight if the density of copper is ρ = 8500 kg/m³. Please result round to one decimal place.
Copper wire has a length l = 820 m and diameter d = 10 mm. Calculate the weight if the density of copper is ρ = 8500 kg/m³. Please result round to one decimal place. - School model
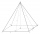 The beech school model of a regular quadrilateral pyramid has a base 20 cm long and 24 cm high. Calculate a) the surface of the pyramid in square decimeters, b) the mass of the pyramid in kilograms if the density of the beech is ρ = 0,8 g/cm³
The beech school model of a regular quadrilateral pyramid has a base 20 cm long and 24 cm high. Calculate a) the surface of the pyramid in square decimeters, b) the mass of the pyramid in kilograms if the density of the beech is ρ = 0,8 g/cm³ - Cross-section 33541
 How many m³ of soil must be moved when digging a straight trench 170 m long, the cross-section of which is an isosceles trapezoid with bases of 150 cm and 80 cm, and arms are 90 cm long?
How many m³ of soil must be moved when digging a straight trench 170 m long, the cross-section of which is an isosceles trapezoid with bases of 150 cm and 80 cm, and arms are 90 cm long? - Cylindrical 28331
 How many crowns will the paint cost to paint a cylindrical container (d = 4.2 m, h = 5.5 m) when about 5 m² of paint is painted from 1 kg of color, and 1 kg of paint costs 115 CZK?
How many crowns will the paint cost to paint a cylindrical container (d = 4.2 m, h = 5.5 m) when about 5 m² of paint is painted from 1 kg of color, and 1 kg of paint costs 115 CZK? - Cone-shaped 23331
 For his birthday, Jirka made a cone-shaped hat out of paper. The side of this cone is 35cm long, and the radius of its base is 20cm. How much dm of paper did Jirka use to make it? Thank you
For his birthday, Jirka made a cone-shaped hat out of paper. The side of this cone is 35cm long, and the radius of its base is 20cm. How much dm of paper did Jirka use to make it? Thank you - Half-cylinder 9961
 The cattle water feeding trough is a half-cylinder with a length of 2 m and a width of 0.8 m. How many m³ of water can be poured into the gutter? How many m² do we need to produce 25 such gutters?
The cattle water feeding trough is a half-cylinder with a length of 2 m and a width of 0.8 m. How many m³ of water can be poured into the gutter? How many m² do we need to produce 25 such gutters? - Rectangular 4547
 How many hours will a tank with a rectangular bottom with a capacity of 105.5 m² and a depth of 2 m be filled when 12 hl of water flows through the pipe in one hour?
How many hours will a tank with a rectangular bottom with a capacity of 105.5 m² and a depth of 2 m be filled when 12 hl of water flows through the pipe in one hour? - Filling the pool
 How many liters of water must be poured into a pool 25m long, 800cm wide, and 20m deep? The pool should be filled to 3/4 of its depth. How many euros will you pay for pool tiling, and a square meter of tiling costs 20 euros?
How many liters of water must be poured into a pool 25m long, 800cm wide, and 20m deep? The pool should be filled to 3/4 of its depth. How many euros will you pay for pool tiling, and a square meter of tiling costs 20 euros? - Quadrilateral 58663
 They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't
They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't - Centimeters 65884
 The plastic bucket has the shape of a cylinder with a diameter of 25 cm and a height of 40 cm. How many square centimeters are needed to produce it? How many liters does it contain when filled 5 cm below the rim?
The plastic bucket has the shape of a cylinder with a diameter of 25 cm and a height of 40 cm. How many square centimeters are needed to produce it? How many liters does it contain when filled 5 cm below the rim? - Surface and volume
 Find the surface and volume of the rotating cone if the circumference of its base is 62.8 m and the side is 25 m long.
Find the surface and volume of the rotating cone if the circumference of its base is 62.8 m and the side is 25 m long. - MO Z9–I–2 - 2017
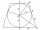
 VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid.
VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid. - Calculate 7246
 The dice have a volume of 80 cm³. Calculate the edge size in mm.
The dice have a volume of 80 cm³. Calculate the edge size in mm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
