Geometry - practice problems - page 7 of 162
Number of problems found: 3232
- Plasticine cuboid
Paul makes a cuboid of plasticine with sides 5 cm, 2 cm, and 5 cm. How many such cuboids will he need to form a cube? - The Earth and Moon
The diameter of the Moon is approximately 1/4 of the diameter of the Earth. What fraction of the volume of the Earth is the volume of the Moon? - EE school boarding
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - Scale model
In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38? - The centroid
The centroid of a triangle ABC is at the point (3,3,3). If the coordinates of A and B are (3, –5, 7) and (–1, 7, – 6) respectively, find the coordinates of the point C. - Prove 2
Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7). - Triangles - segments
How many triangles can be formed with segments measuring one and 2/3 mm one 3/4 mm and 2 1/2 mm - Freezing
A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5°C per hour.What will be the room temperature 12 hours after the process begins? - The temperature 39
The temperature outside is currently 10 degrees, dropping at an average rate of 2 degrees per hour. If the temperature continues to drop at this rate, what will the temperature be in 7 hours? - Iron ball 2
What is the mass of the iron ball with a diameter of 1,0 dm? The density of iron is 7870 kg/m³. . - A cube 4 A cube of edge 5 cm is cut into cubes, each of edge 1 cm. Find the ratio of the total surface area of one of the small cubes to that of the large cube.
- The radius 3
The radius of a solid circular cylinder decreases by 20% and its height increases by 10% . Find the percentage change its : (a) volume (b) curved surface area. - The temperature 38
The temperature has been dropping 2 degrees every hour, and the temperature at 10:00 AM was -15 degrees Fahrenheit. At what time was the temperature 0 degrees Fahrenheit? - Spheres - ratios
The surface area of two spheres are in the ratio 1 : 4 . Find the ratio of their volumes. - Trigonometric fx
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - A boy 5
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - Building shadow
When Sun's altitude 30° above the horizontal, then find the length of the shadow of a 50 m high of a building . - Angle and slope
Find the angle between the x-axis and the line joining the points (3, -1) and (4,-2) . - Vertical components
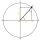
Find the horizontal and vertical components of the vector which has magnitude 750 as shown in the following figure. - Hourglass ticks
The hourglass ticks three times in 5 minutes. How many times do they spill in 2 hours?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
